Romberg.html

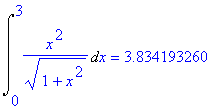
>    restart;

Romberg := proc()
local f, a, b, h, i, j, n, sum, R, xi, i1,i2,j1,j2;
printf("***** Author: Mengnien Wu *********************************\n");
printf("* Complete the Romberg table R of size n - each entry     *\n");
printf("* approximates the definite integral of a given function. *\n");
printf("***********************************************************\n");
printf("\nEnter the integrant in terms of variable x:\n");
f := scanf("%a")[1]; f := unapply(f,x);
printf("Enter lower limit:\n"); a := scanf("%a")[1];
printf("Enter upper limit:\n"); b := scanf("%a")[1];
printf("Enter n:\n");           n := scanf("%d")[1];
printf("By Maple command,\n");
print(Int(f(x),x=a..b)=evalf(int(f(x),x=a..b)) ); # Maple commands
a:= evalf(a,16); b:= evalf(b,16); # 16 digit accuracy

h := array(1..n);
h[1] := evalf(b-a,16);
for i from 2 to n do
  h[i] := evalf(h[i-1]/2,16);
od;

R := array(1..n,1..n);
for i from 1 to n do
  for j from i+1 to n do
    R[i,j] := 0;
  od;
od;
R[1,1]:=evalf((f(a)+f(b))*h[1]/2,16);
for i from 2 to n do
  xi :=evalf(a-h[i],16);
  sum := 0;
  for j from 1 to 2^(i-2) do
    xi := evalf(xi+2*h[i],16);
    sum := evalf(sum+f(xi),16);
  od;
  R[i,1]:= evalf((R[i-1,1]+h[i-1]*sum)/2,16);
od;

for j from 2 to n do
  for i from j to n do
    R[i,j]:=evalf(R[i,j-1]+(R[i,j-1]-R[i-1,j-1])/(4^(j-1)-1),16);
  od;
od;

printf("Enter i1,i2 to view Romberg table {R[i,j], i=i1..i2, j=i1..i2}:\n");
i1:=scanf("%d")[1]; if i1<1 then i1:=1; fi;
i2:=scanf("%d")[1]; if i2<i1 then i2:=i1; fi;
if i2>n then i1:=min(i1,n); i2:=n; fi;
for j from i1 to i2 do
  printf("%12d",j);
od;
printf("\n");
for i from i1 to i2 do
  printf("%2d:",i);
  for j from i1 to i do
    printf("%12.8f",R[i,j])
  od;
  printf("\n");
od;
end:

> Romberg();

***** Author: Mengnien Wu *********************************

* Complete the Romberg table R of size n - each entry     *

* approximates the definite integral of a given function. *

***********************************************************

Enter the integrant in terms of variable x:

> x^2/sqrt(1+x^2)

Enter lower limit:

> 0

Enter upper limit:

> 3

Enter n:

> 5

By Maple command,

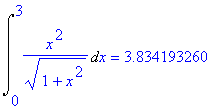
Enter i1,i2 to view Romberg table {R[i,j], i=i1..i2, j=i1..i2}:

> 1 5

           1           2           3           4           5

 1:  4.26907484

 2:  4.00665058  3.91917583

 3:  3.88288228  3.84162618  3.83645620

 4:  3.84642196  3.83426851  3.83377800  3.83373549

 5:  3.83725052  3.83419337  3.83418836  3.83419487  3.83419668

>